Time helps us bring order to various events in a distributed system. Time helps us in determining what happened when and how long did some event take. The hard part is when we introduce the concept of a shared clock across nodes in a distributed system. In this post, we shall look at time and clocks and how we can order events across nodes in the system. We shall also look at what issues that occur when having a shared global clock and other strategies to use to bring order to events — within a distributed system. Also, note that we will not be discussing about time/timezones on a single node and our discussion is only about time on distributed systems.
There are two ways to measure time in a system. One is duration — that answers questions like how long did something take and the other is point-in-time — that answers questions like when something did take place. Time elapsed between a method call and timeout of a network call are examples of duration. Whereas, timestamps in a log file and expiration time of a certificate are examples of point-in-time.
Bringing global time/clock to a distributed system, helps us account for the order of events that happened within it. It also helps us answer questions like: whether event A happened before event B, if event C is a predecessor or successor to event D, when some event E occurred relative to others etc. Sometimes, correctness depends on the correct ordering of the events — in the case of a distributed database or in trying to acquire a distributed lock or in failure detection across various components. As we shall see later, this ordering information can help a distributed system function correctly — in case of failures.
There are two types of clocks that we use on distributed systems:
- Physical Clocks - Time-of-Day clocks/Monotonic clocks
- Logical Clocks - Counters implemented in some arbitrary way
Physical Clocks #
The physical clocks used in computers make use of a hardware device which is usually a quartz crystal oscillator. This device produces a signal at a predetermined/predictable frequency and this is used to calculate the time. This is not foolproof though since such devices are not perfectly accurate and changes in temperature results in clock drifts from other machines in the cluster. And so, we cannot have a consistent notion of time across nodes.
Network Time Protocol (NTP) was developed to adjust a machine’s clock according to a time reported by a group of servers. The NTP servers usually get their time from an accurate source like a GPS receiver or similar. But, you should note that NTP again is not fool proof with Time-of-Day clocks (Monotonic clocks only go forward and hence do not need synchronization). Due to the adjustment of a machine’s clock using NTP, can result in a clock going back in time — causing your application from not working as expected and if the drift is too much, the machine’s clock might not even be changed. Also, since NTP synchronization happens over a network — the network delay can also affect the accuracy of the time returned. Moreover, NTP can also stop working due to a network outage and has with it the same problems seen in a network. To get accurate time, Precision Time Protocol and others were developed that made use of GPS receivers to get the time on each node. Although this is sometimes not practical due to the cost/effort involved.
There are also Leap seconds that Time-of-Day Clocks/NTP needs to contend with. This is a periodic adjustments made to UTC due to the long-term slowdown in the Earth’s rotation. This adjustment results in a minute having 61 or only 59 seconds. This can at best cause errors in your applications and at worst crash or corrupt data. Some examples and details of such instances can be found here and here. More information about this practise and a detailed explanation can be found here. In fact, Meta suggests to stop accounting for Leap seconds altogether and their points seem valid.
Most languages/frameworks have support for these two kinds of physical clocks. Let us look at each of them.
Time-of-Day Clocks #
The Time-of-Day clock returns you the date and time based on your locale. This is also known as the wall clock and using such a clock we can answer point in time questions. For example, the time on the log files are an example of a point in time that an operation happened then.
In Linux, if you want the wall clock time with nanosecond precision, you can use the clock_gettime() API provided. The clock type needs to be specified as CLOCK_REALTIME and this gives you the time since the epoch.
The Time-of-Day clock is local to that machine but can be synchronized through NTP so that the timestamp from one machine will mean the same when matched with an another machine. But it is important to note, and as seen above, that even when configured with NTP, time can move backwards and this behaviour can cause unintended results. Also, most OS allow you to change the Time-of-Day clock and this can again cause problems in your applications, when programmed without any such assumptions.
Monotonic Clocks #
Monotonic clocks helps us measure duration in our applications. The time between a start of an operation and the end of the same operation, is an example of a duration. A Monotonic clock measures time since some “point in the past”. This clock is useful because it is always guaranteed to move forward and cannot jump back in time and hence your application has the same context.
In Linux, you can use the clock_gettime() API provided with the clock type specified as CLOCK_MONOTONIC to give you the time. You can also specify the clock type as CLOCK_MONOTONIC_RAW to get a suspend-aware monotonic time.
The Monotonic clock is local to a machine and one machine’s value cannot be compared to a value from another machine, as the value of the clock is meaningless and out of context when compared within an another machine’s monotonic clock.
To summarize the physical clocks, consider the loosely constructed code:
/*
* Wall Clock Time
*/
clock_gettime(CLOCK_REALTIME, &ts_start);
perform_work(); // CLOCK CAN GO BACK IN TIME MEANWHILE (NTP or otherwise)
clock_gettime(CLOCK_REALTIME, &ts_end);
elapsed = ts_end.tv_nsec - ts_start.tv_nsec; // CAN BE NEGATIVE
/*
* Thic can be COMPARED in a cluster, if NTP synced and working correctly
*/
clock_gettime(CLOCK_REALTIME, &some_time);
/*
* Monotonic Clock Time
*/
clock_gettime(CLOCK_MONOTONIC, &ts_start);
perform_work(); // CLOCK CAN ONLY GO FRONT
clock_gettime(CLOCK_MONOTONIC, &ts_end);
elapsed = ts_end.tv_nsec - ts_start.tv_nsec; // GUARANTEED TO BE POSITIVE
/*
* Thic cannot be COMPARED across machines
*/
clock_gettime(CLOCK_MONOTONIC, &some_time);
More information about the clock_gettime() API can be found here.
Modern Improvements #
Recently, distributed systems have started to make use of clock readings that have a confidence interval associated with it. This confidence interval is determined by the manufactures of the time source or determined with practice. The confidence interval usually consists of a lower bound and an upper bound and the right time is somewhere in the middle. Google Spanner provides a TrueTime API that produces such an interval for the time returned. And then, there are some systems that assume clocks within a cluster are synchronized perfectly with each other. This might lead to situations where stale data overwrites the latest data (Last write wins), but again that is accounted for within the system and stated explicitly. Facebook’s Cassandra is one such example of such an system.
Physical clocks can be used to assign partial order — events on each system are ordered but events cannot be ordered across machines using a physical readings of a clock. It is good practice to not make the assumption that the physical timestamps across machines can be matched/compared with each other.
Ordering #
Before jumping into Logical Clocks and its uses in Distributed Systems, let us define ordering within the same context. This will help when discussing about these clocks next.
Knowing the ordering of events is crucial to correctness in a distributed system. One such important ordering is called the Causality or Happens-Before. Consider the below:

Fig 1: Events in a system
Suppose you have two events - e1 and e2. And we say e1 happened before e2, denoted by e1 —> e2. This ordering tells us:
- e1 could have maybe or potentially caused e2
- e2 could not have caused e1
These types of ordering are very useful when reasoning about Distributed Systems. The orderings can explain why the system is in a given state. This will also help in case of diagnosing errors that may occur within the system.
Now coming to the actual definition of the happens-before relationship on two events e1 and e2 (Denoted by e1 —> e2), in the case of multiple nodes:
- e1 and e2 happen on the same node and e1 is before e2. This means that e1 happened before e2 and is denoted as e1 —> e2
- e1 = send(msg) and e2 = recv(msg), where msg is the same and is assumed the communication happens between two different nodes, then e1 happened before e2 and is denoted as e1 —> e2
- If e1 —> e2 and e2 —> e3, then due to transitivity, we can say e1 —> e3
If two events display any of the above, we say that they exhibit a happens-before relation.
As an example, consider the following events in a distributed system:
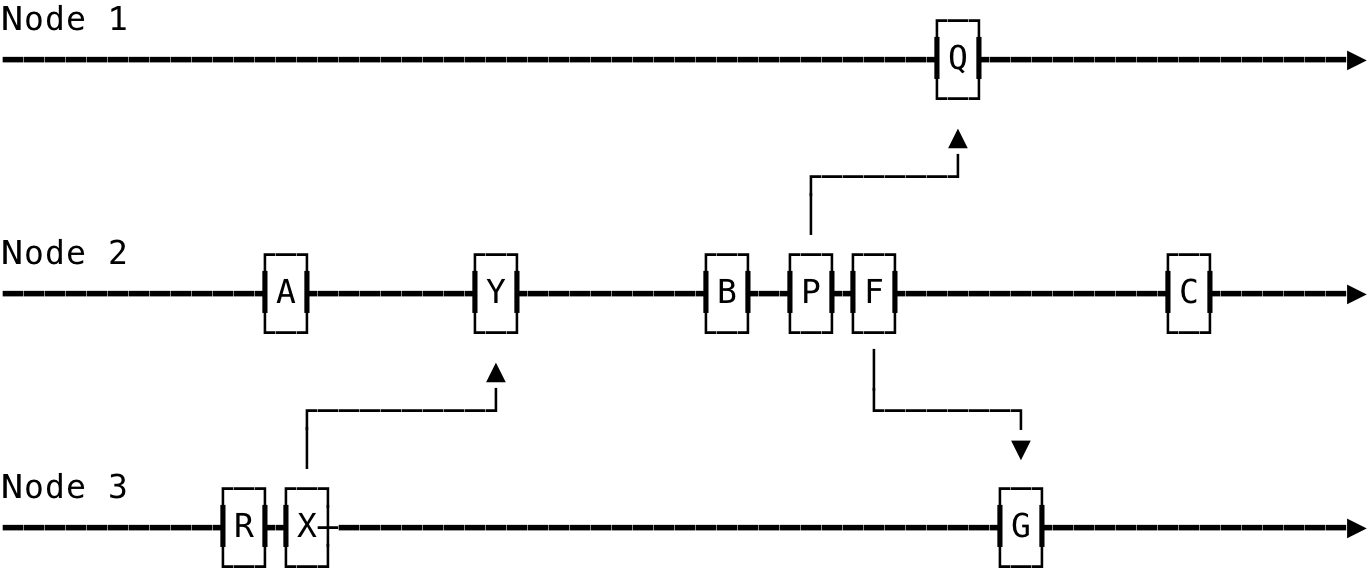
Fig 2: Example: Happens-Before
Here, X —> Y since X = send(m1) and Y = recv(m1) and the same reason holds for P —> Q. We can also say A —> Y, since the event Y happened on event A, on the same node. X —> Q holds due to transitivity.
In the above, we cannot relate events A and R through happens-before/causal relationship, because neither A —> R or R —> A is true. Hence we say event A and event R are concurrent and is denoted as A || R. Events A and R are also said to be independent. Similarly, the events F and G are independent and is denoted as F || G.
Causal Anomaly occurs when we cannot determine the causal order of the events and this leads to inconsistencies in the system. This can been seen below:
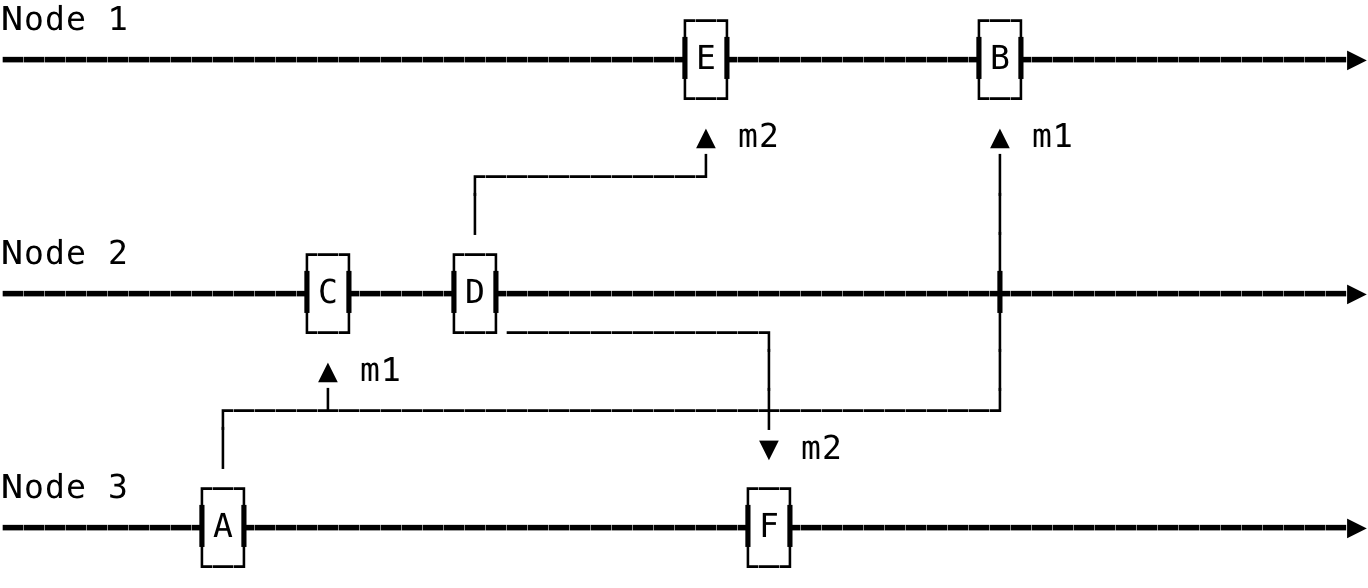
Fig 3: Example: Causal Anomaly
Here, m1 originates first but is delivered after m2 on Node 1 (This can be due to a slow network for one). This breaks assumptions on Node 1 that m2 should be ordered after m1 and might lead to situations where m1 might end up overwriting a value set through m2 due to incorrect ordering assumptions where m2 being the actual latest value.
Happens before relationship is a Partial Order (Although it is irreflexive and hence known as an irreflexive partial order). More details on Partial Order can be found here.
Physical Clocks, seen earlier, are inconsistent with causality and that is the need for Logical Clocks in distributed systems, that we will look at now.
Logical Clocks #
Logical clocks are implemented using some counters in the system. Mostly, logical clocks count the number of events that occurred in the machine and like monotonic clocks, logical clocks only move forward.
Logical clocks are designed to capture causal dependencies or happens before relationship. In short, given two events e1 and e2, and we know that e1 happened before e2, we want T(e1) < T(e2), where T(e) is the timestamp of event e. This helps captures the causal/happens-before relation seen earlier.
The most used logical clocks within an distributed systems are: Lamport Clocks and Vector Clocks. We will now look at them in detail.
Lamport Clocks #
Lamport clocks are used to bring in causal order to events distributed across a cluster. The algorithm is based on the classical paper by Leslie Lamport.
Lamport Clocks are consistent with causality - because if A happens before B (A —> B), then LC(A) < LC(B).
The algorithm works as follows:
// Each node has T, resembling a logical timestamp
T = 0
for event in local node:
T = T + 1
When sending a message M:
T = T + 1
send(T, M)
When receiving a message (T', M):
T = max(T, T') + 1
send(M) to the underlying service
Using such a timestamp, now if event e1 happened before event e2 (e1 —> e2), then LC(e1) < LC(e2) where LC() is just the value of T, after the events e1 and e2.
However, only given LC(e1) < LC(e2), we cannot infer that e1 happened before e2 — because both the events e1 and e2 can be concurrent (e1 || e2). We can only rule out e2 happened before e1 — else, LC(e2) would be less than LC(e1).
It is also possible that LC(e1) == LC(e2) for any two events e1 and e2, that happened on different nodes in the cluster. Usually, to get unique ordering of the events in a cluster, we can combine [LC(e), N(e)] where N(e) is the node ID at which the event originated.
Below is the Lamport Clock values of events across a cluster:
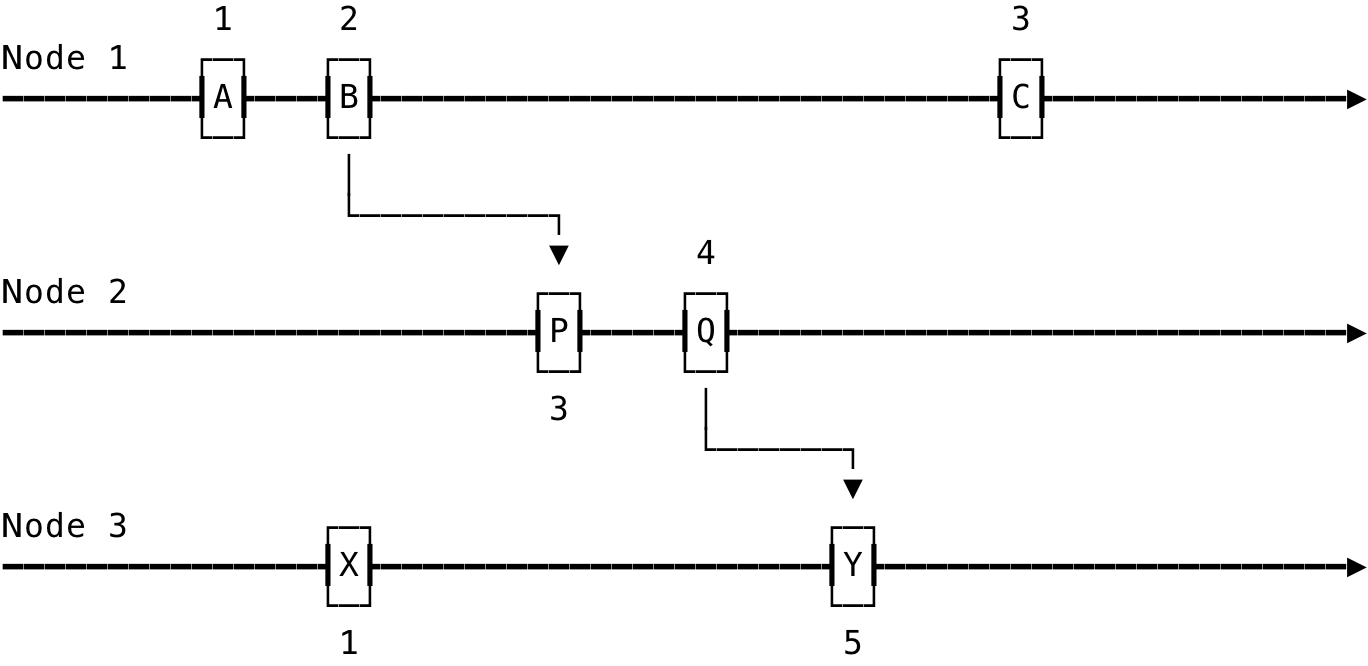
Fig 3: Example: Lamport Clock
As discussed earlier, LC(X) < LV(B) does not mean that X —> B but are actually independent events (X || B). And LC(A) = LC(X) since they are independent and happened on different nodes.
A compute intensive way to find out causality is to graph reach events in the space time diagram, that we have used in our figures.
We can definitely use Lamport Clocks to rule out events that have not caused other events, like X and P in the above space time diagram. And, if we want to detect concurrent events and strict ordering between events, we need vector clocks.
Popular databases like MongoDB and CockroachDB use Vector Clocks in their implementations.
Vector Clocks #
Vector Clocks helps us overcome the limitations of Lamport Clocks. Vector Clocks are consistent with causality/Happens-before. This means given two events e1 and e2, If e1 —> e2 (e1 happend before e2), then VC(A) < VC(B). The difference with Lamport Clocks, seen earlier, is that — given VC(A) < VC(B) then e1 —> e2 is also true (e1 happened before e2). The relationship is said to be a strict since it goes both ways. Hence, Vector Clocks are said to characterise causality.
Before we look at the algorithm used for Vector Clocks, the following is the representation used in the algorithm:
- If there are N nodes in the system — The timestamps are denoted using a vector such as, VC = [V1, V2, …, VN]
- The timestamp of an event e1 is denoted as, VC(e1) = [T1, T2, …, TN]
- Ti is the number of events observed on Node i
With the representation in place, the core algorithm is as follows:
// Each node has T, resembling a logical timestamp
T = [0, 0, 0, ..., 0]
for event in local node i:
T[i] = T[i] + 1
When sending a message M, on node i:
T[i] = T[i] + 1
send(T, M)
When receiving a message (T', M) on node i:
for j till N:
T[j] = max(T[j], T'[j])
T[i] = T[i] + 1
send(M) to the underlying service
This can be explained with the below example:
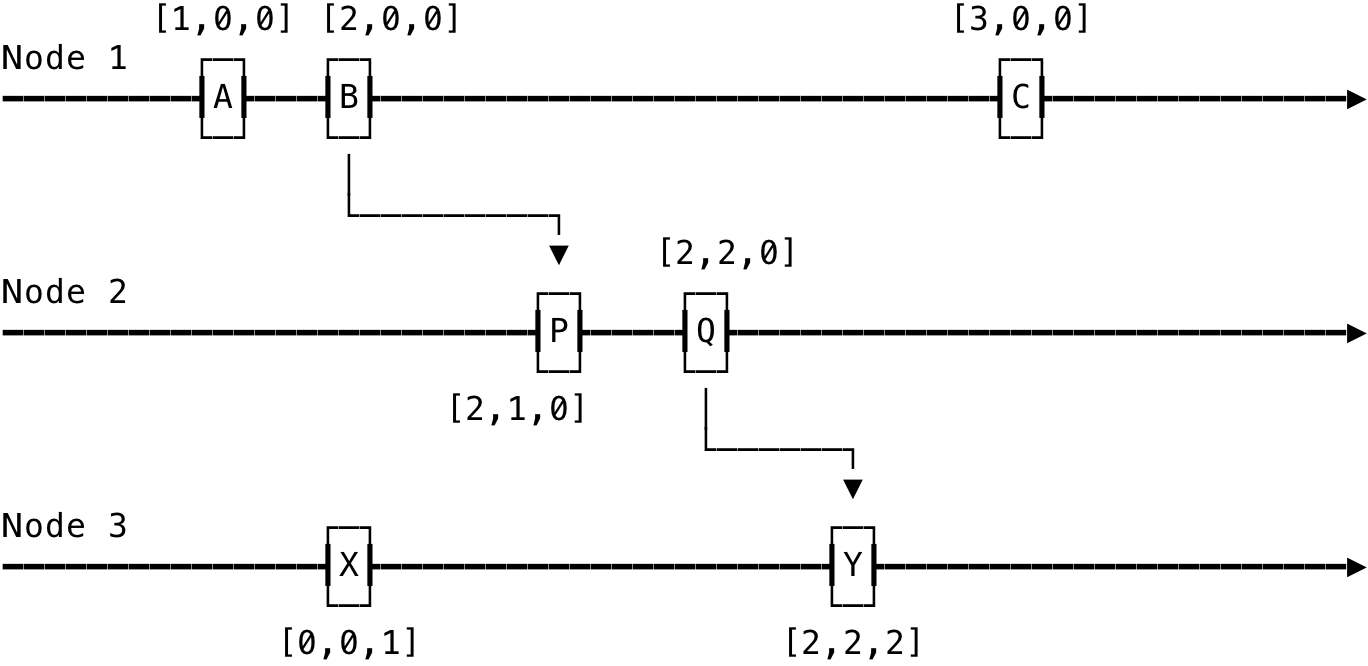
Fig 4: Example: Vector Clock
In the above, the Vector Clock values of an event e1 represents a set of events that happened before it. For example, VC(Y) = [2, 2, 2], which denotes — there are two events from Node 1 before it, two events from Node 2 before it and it is the second event on Node 3.
Generally, to compare two Vector Clocks — say VC(e1) and VC(e2):
- VC(e1) ≤ VC(e2), if VCe1 <= VCe2, for all i in {1, …, N}
- VC(e1) < VC(e2) (Strict), then VCe1 <= VCe2, for all i in {1, …, N} and e1 != e2.
Then,
- VC(e1) < VC(e2) implies e1 —> e2 and this also goes the other way — e1 —> e2 also specifies VC(e1) < VC(e2)
- VC(e1) ≰ VC(e2) and VC(e2) ≰ VC(e1) implies e1 || e2 (Parallel or Independent events)
In the above example figure, Q —> Y since [2, 2, 0] ≤ [2, 2, 2] and the same holds when we say B —> Y since [2, 0, 0] ≤ [2, 2, 2]. We can also say A || X since [1, 0, 0] ≰ [0, 0, 1] nor [0, 0, 1] ≰ [1, 0, 0] (VC(A) ≰ VC(X) nor VC(X) ≰ VC(A))
Dynamo actually uses Vector Clocks to capture causality between changes in the same object. In practise, Vector Clocks are somewhat hard to implement and needs perfect information to make sense. It is also computationally intensive than other logical schemes.
That’s it. For any discussion, tweet here.
[1] For fun, see how many of your assumptions about time are invalid. And this is only on a single node - https://infiniteundo.com/post/25326999628/falsehoods-programmers-believe-about-time
[2] http://book.mixu.net/distsys/single-page.html#time
[3] https://en.wikipedia.org/wiki/Lamport_timestamp
[4] https://en.wikipedia.org/wiki/Vector_clock